David Sklansky Starting Hands

The table below illustrates the overview of the Sklansky groups and possible poker hands: 1 - AA, AKs, KK, QQ, JJ 2 - AK, AQs, AJs, KQs, TT 3 - AQ, ATs, KJs, QJs, JTs, 99 4 - AJ, KQ, KTs, QTs, J9s.

Author David Sklansky

Find out how to qualify for this book in the Two Plus Two poker bonus program

• Hold'em Poker is a revision of Sklansky's classic from 1976. It was the first authoritative poker book to actually give starting hands in hold'em. Sklansky arranged the hands into eight groups and gave recommendations on which ones to open with depending on position. In this edition he has revised the groups and corrected some minor errors.
• This is the first non paired starting hand on the list, and as such, it includes information on suitedness. And as you can see by scrolling down a bit, Ace King suited is actually a much better hand than its off suit equivalent. Poker players love big slick as much as any other hand in the game besides pocket aces. This has something to do with.

Synopsis of the Book Hold'em Poker

Updated for today's double blind structure. Contains the most up-to-date Sklansky Hand Rankings available. 1997 Edition Second Printing 2001 This is the first Hold'em book you should read before playing in any public poker room.-videopro Hold'em Poker by David Sklansky is must reading for anyone planning to play in Nevada, California, or any place else where hold'em is offered including a home game. This was the first definitive work on hold'em poker and was originally published in 1976. Yet, it is still one of the best-selling poker books available. The text is designed for someone relatively new to the game, but it still contains much sophisticated material.

The text is probably best known for the Sklansky Hand Rankings, which made the game much simpler to quantify and understand. Some of the topics include the importance of position, the first two cards, the key 'flops,' strategy before the flop, semi-bluffing, slowplaying, check raising, head-up on fifth street, and how to read hands. Not only was this text, which is Sklansky's first work, a major contribution to the explosive growth of this game, it is also a book that should still be read by all serious players.

Excerpt from the Book Hold'em Poker: Position

Introduction

A player's position is more important in Hold'em than in any other poker game. Only draw poker is close. In both draw and Hold'em the dealer acts last and the man 'under the gun' acts first on each betting round. (In some forms of draw poker, the opener, rather than the man under the gun, acts first after the draw, which somewhat diminishes the dealer's advantage.) However, Hold'em has four betting rounds as opposed to draw poker's two. This fact serves to compound the advantages of late position and the disadvantages of early position.

Some Considerations

Why are these considerations so important? Here is an analysis: First, take the play before the flop. If you call in early position, you are subjecting yourself to one or more raises behind you. The earlier your position the more risk you are taking. If you wouldn't have called if you knew there was a raise behind you, you have now been forced to put $20 dollars in before the flop with a hand that doesn't justify it. If you fold without calling the raise, you have given up $10 dollars without seeing a card. Also some hands are only worth playing if there are many other callers. In early position you are just guessing about how many people will play.

Other considerations involve the fact that if you are in early position or under the gun, you will remain there throughout the hand. Assume now that it is sometime after the flop. Once again, if you are in last position with only a fair-to-good hand, and the first player bets, there can be no raise behind you. Those players in middle position have no such comfort. If you have a 'big hand' in this spot, your advantage in being last is even greater. This is best seen by comparing your situation with being first with a big hand. If you were first you might try to check and raise, but if it doesn't work you have lost a few bets from those that would have been called you, and given a free card to those that wouldn't. Being last, you will always be able to bet even if you don't get the opportunity to raise. If you are in middle position with a big hand, you still have problems. If no one has yet bet and it is up to you, you must decide whether to risk 'sandbagging.' Also, if someone has bet in front of you, a raise will drive players out behind you. These extra bets lost, really add up.

Even if the pot narrows down to two players, these positional considerations still apply, maybe more so. Suppose you are last to act and have a big hand. Once again if your opponent bets you can raise. If he doesn't bet, you do. lf you are first with the same hand, you can only make two bets if a check-raise works. If it doesn't, you have cost yourself a bet. If instead you come right out betting with this hand in first position, you lose a bet when a check raise would have worked, but he now just calls. If your hand is only mediocre, it is once again advantageous to be last. If you can't call a bet, you still may get a free card (which could wind up beating him) if he chose to check a hand which you know is better than yours. However, if you are first with this same hand, it is unlikely that he will still check after you check. Finally, even if your hand is somewhere in the middle (good, but not great) it is better to be last. While it is true that you will bet in either position, if he is first, and comes out betting, you will simply call him. If you were first in this spot, you would bet and he might raise. The importance of these extra bets that may be saved or gained by being in late position cannot be overemphasized. Never forget that in poker we are trying to win money -- not a lot of pots.

It is true as some sharp readers may have realized, that occasionally it is an advantage to be in early position. Sometimes you want to drive players out to make your hand stand up. Only raising in early position will do this. Secondly, if you are first with 'a lock' you may make three bets by betting and then reraising. However, these exceptions do little to change the general principle that it is better to be last. (This, by the way, is even more true when the check and raise feature is not allowed.)

How then do we make use of this information? Later on in the Strategy chapter, I will discuss situations after the flop where your position determines your action. However, the main point of this chapter is to show why you must take your position very much into account when you are deciding whether to play a specific hand or not. Any starting hand can become a winning hand when all the cards are out. However, some hands doso more than others. For this reason, the lesser hands can be played only in late position. Not simply because you are in little danger of a raise behind you before the flop, but also because of the bets that are gained (or saved) when you turn a hand in this position. Conversely, the opposite considerations apply in early position. Therefore, the earlier your position, the better your first two cards must be to play. But what are good starting hands?

Editor’s Note: This article was first published in the March, 2014 issue.

In part one, we looked at Norman Zadeh’s approximate game theory optimal solution to a heads up, pot-limit, one round poker game. Both players ante $1, the first player checks or bets $2 and if he checks, the second player bets either $2 or checks also. There are no raises.

Zadeh worked out that the first player should bet his top 14% and bluff with his bottom 7%. He should check and call with hands between 14 and 50 and check and fold with hands between 50 and 93. The second player should call with the top half of his hands and if checked to bet the top 30% and bluff with the bottom 15%. He would fold hands 50-85.

When both players use Zadeh’s strategy, the first player has an EV of about -8.5 cents.

What if one of the players differs substantially from this approximant game theory optimal strategy? To give you an idea of what happens, take a look at the following example. Suppose the first player uses the strategy where he bets the top 40% and the bottom 32% of his hands and checks and calls with the remaining hands, which are between 40 and 68. Against him, would player two’s GTO strategy, as specified by Zadeh, still work? Certainly, that strategy is far from the best when facing player one. For instance, player two should never bluff against player one since he will always be called. Secondly, when player one bets, the Zadeh strategy for player two will have him folding far too often. Finally, if player one checks, player two should value bet way more than his top 30%.

In spite of all these flaws, mathematicians contend that GTO does at least as well against bad players as it does against other GTO players. Thus, they would predict that sticking with Zadeh’s strategy will win player two at least 8.5 cents per hand. We will see if that’s right in part three of this essay.

For now, however, I think it would be a good exercise to come up with the perfect counter strategy to player one given that you know his strategy. Again, his strategy is to bet hand 0-40 and 68-100 and to check and call with the rest. Before reading further, see if you can do this yourself.

Suppose player one checks, how many hands can player two bet for value? Well certainly, he can bet 0-40, as they are all certain to win. But, he can also bet another 14% and still be the favorite. Do you see why? Player two will be calling from 40-68. If player one bets, we need to call with hands that have a better than 1/3 chance of winning since we are getting 2:1 odds. Notice that hand 68 is an easy call since it loses to hands 0-40, but beats the bottom 32% that he also bets. The fact is that player two can call with hands all the way down to 76. With that hand, he will lose to all of player one’s value bets and even to some of player one’s “bluffs”. Still though, he is only a 48:24 underdog.

We will now use the method I showed you in part one to calculate the EV of player one when facing the perfect counter strategy.

● If player one has hand 0-40 and player two has hand 0-40, there will be a bet and a call and they will break even. This happens 16% of the time and the EV is 0.

● If player one has hand 0-40 and player two has hand 40-76, there will be a bet and a call and player one will win $3. This will happen 14.4% of the time and the EV is 43.2 cents.

● If player one has hand 0-40 and player two has hand 76-100, there will be a bet and a fold and player one will win $1. This will happen 9.6% of the time and the EV is 9.6 cents.

● If player one has hand 40-54 and player two has hand 0-40, there will be a check and a call and player one will lose $3. This will happen 5.6% of the time and the EV is -16.8 cents.

David Sklansky Starting Hands Book

● If player one has hand 40-54 and player two has hand 40-54, there will be a check and a call and they will break out even. This will happen 1.96% of the time and the EV is 0.

● If player one has hand 40-54 and player two has hand 54-100, it will go check-check and player one will win $1. This will happen 6.44% of the time and the EV is 6.44 cents.

● If player one has hand 54-68 and player two has hand 0-54, it will go check-call and player one will lose $3. This will happen 7.56% of the time and player one will lose 22.68 cents.

● If player one has hand 54-68 and player two has hand 54-68, it will go check-check and they will break even. This will happen 1.96% of the time and the EV is 0.

● If player one has 54-68 and player two has 68-100, it will go check-check and player one will win $1. This will happen 4.48% of the time and the EV is 4.48 cents.

● If player one has hand 68-76 and player two has hand 0-68, it will go bluff-call and player one will lose $3. This will happen 5.44% of the time and the EV is -16.32 cents.

● If player one has 68-76 and player two has 68-76, it will go bluff-call and they will break even. This will happen .64% of the time and the EV is 0.

● If player one has 68-76 and player two has 76-100, it will go bluff-fold and player one will win $1. This will happen 1.92% of the time and the EV is 1.92 cents.

● If player one has 76-100 and player two has 0-76, it will go bluff-call and player one will lose $3. This will happen 18.24% of the time and the EV is -54.72 cents.

● If player one has 76-100 and player two has 76-100, it will go bluff-fold and player one will win $1. This will happen 5.76% of the time and the EV is 5.76 cents.

When you add up player one’s EVs, it comes to -39.12 cents, much worse than how he would do if he stuck to his GTO strategy, even against a world class player.

David Sklansky Starting Hands Church

To be continued…..

David Sklansky Starting Hands Youtube

David Alan Sklansky

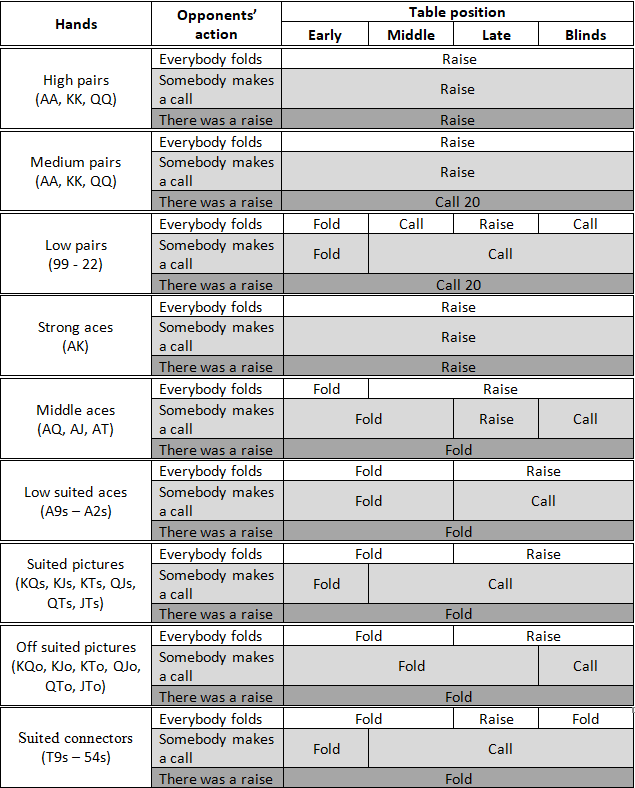
David Sklansky Starting Hand Chart